1
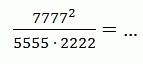
A) 1 Б) 7/10 В) 49/10 Г) 77/110 Д) 49
2
Юля бросила пять кубиков и получила 19 очков. Какое максимальное количество шестёрок она могла выбросить?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
3
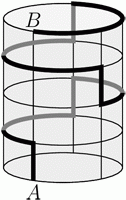
Цилиндрическая банка имеет высоту 15 см, а периметр ее круглого основания равен 30 см. Муравей ползёт по поверхности банки из точки А на нижнем основании в точку В на верхнем основании, как показано на рисунке. Все участки пути либо вертикальные, либо горизонтальные по дугам окружности. Какую длину имеет путь муравья?
A) 45 см Б) 55 см В) 60 см Г) 65 см Д) 75 см
4

У Эммы есть четыре фломастера разного цвета. Она хочет раскрасить трёхполосный прямоугольный флаг так, чтобы каждая полоса была одного цвета, а любые две соседние полосы ─ разного цвета. Сколькими способами она может это сделать?
A) 24 Б) 27 В) 32 Г) 36 Д) 64
5
Натуральное число n будем называть 2-простым, если оно имеет ровно три различных натуральных делителя, а именно 1, 2 и само n. Сколько существует различных 2-простых чисел?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
6
Сколько различных пар (x; y), где x, y – натуральные числа, удовлетворяют уравнению
x + 2y = 210
A) 29 - 1
Б) 29
В) 29 + 1
Г) 29 + 2
Д) 0
7
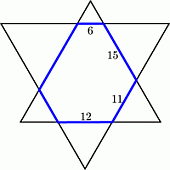
Два равносторонних треугольника в пересечении образуют шестиугольник, противоположные стороны которого параллельны. Длины четырёх сторон этого шестиугольника указаны на рисунке. Чему равен периметр этого шестиугольника?
A) 64 Б) 66 В) 68 Г) 70 Д) 72
8

Квадрат площадью 84 разбит на четыре квадрата. Верхний левый квадрат окрашен в чёрный цвет. Нижний правый квадрат также разбит на четыре квадрата, левый верхний из которых снова окрашен в чёрный цвет, и так далее, до бесконечности. Чему равна площадь чёрной части исходного квадрата?
A) 24 Б) 28 В) 31 Г) 35 Д) 42
9

Миша вписывает каждое из чисел от 1 до 9 в девять клеток полоски (в каждую – ровно одно число). Он хочет, чтобы суммы чисел в любых трёх последовательных клетках были кратны 3. Числа 7 и 9 Миша уже вписал так, как показано на рисунке. Сколькими способами он может заполнить оставшиеся клетки?
A) 9 Б) 12 В) 15 Г) 18 Д) 24
10
Какой цифрой заканчивается число, равное произведению
(55 + 1)(510 + 1)(515 + 1)?
A) 1 Б) 2 В) 4 Г) 5 Д) 6
11
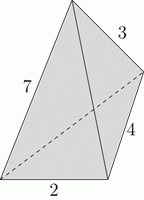
Треугольная пирамида имеет рёбра целочисленной длины. Длины четырёх из этих рёбер показаны на рисунке. Чему равна сумма длин двух других рёбер?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
12
Пусть n – натуральное число. Выражение n! означает произведение всех натуральных чисел от 1 до n включительно.
Например, 4! = 1 ∙ 2 ∙ 3 ∙ 4 = 24.
Чему равна сумма цифр числа N, если N! = 6! ∙ 7! ?
A) 1 Б) 2 В) 4 Г) 8 Д) 9
13
Пусть графики всех функций вида
y = x3 + 3x2 + ax + 2a + 4
проходят через одну точку, независимо от значения а. Чему равна сумма координат этой точки?
A) 2 Б) 4 В) 7 Г) 8 Д) другой ответ
14
Сумма пяти чисел a1, a2, a3, a4, a5 равна S.
Для любого k, 1 ≤ k ≤ 5, верно равенство ak = S + k. Чему равно значение S?
A) 15/4
Б) -15/4
В) -15
Г) 15
Д) другой ответ
15
Сколько различных пар (m; n), где m, n – целые числа, удовлетворяют неравенству
|2m - 2023| + |2n - m| ≤ 1 ?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
16
В кинотеатре в первом ряду сидят 23 животных. Каждое из них либо бобёр, либо кенгуру. У каждого животного в этом ряду хотя бы один из соседей – кенгуру. Какое наибольшее количество бобров может быть в этом ряду?
A) 7 Б) 8 В) 10 Г) 11 Д) 12
17
Число 556 можно представить в виде nn. Чему равно n?
A) 530 Б) 56 В) 55 Г) 30 Д) 11
18
Леон нарисовал на поверхности прямоугольного параллелепипеда замкнутый путь. В каком из следующих ответов может быть изображена развёртка поверхности данного параллелепипеда?

19
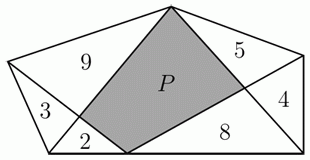
Пятиугольник разбит на несколько частей, как показано на рисунке. Числа внутри треугольников указывают их площади. Чему равна площадь серого четырехугольника?
A) 15 Б) 15,5 В) 16 Г) 17 Д) 18
20
Сколько делителей числа 220 ∙ 323 не являются делителями числа 210 ∙ 320 ?
A) 13 Б) 30 В) 273 Г) 460 Д) другой ответ
21
Две функции f(x) и g(x), заданные на множестве действительных чисел, удовлетворяют уравнениям
f(x) + 2g(1 - x) = x2 и
f(1 - x) - g(x) = x2
при всех значениях x. Найдите формулу, задающую функцию f(x).
A) 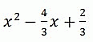
Б) 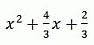
В) 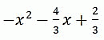
Г) x2 - 4x + 5
Д) такой функции не существует
22
В соревнованиях по боулдерингу 13 альпинистов соревнуются в трёх категориях. Оценка каждого участника является произведением его рейтингов в трёх категориях. Например, если спортсмен занимает 4-е, 3-е и 6-е места, его оценка будет равна
4 • 3 • 6 = 72.
Чем выше оценка, тем ниже общий рейтинг на соревнованиях. Анна заняла 1-е место в двух категориях. Какой самый низкий общий рейтинг у неё может быть?
A) 2-й Б) 3-й В) 4-й Г) 5-й Д) 6-й
23
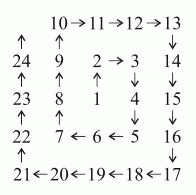
Спираль из последовательных натуральных чисел строится, начиная с 1, как показано выше. Если построение спирали будет продолжено, то как в ней будут располагаться числа 625, 626 и 627?
24
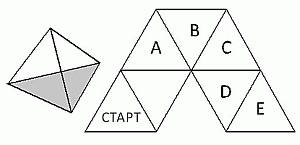
У правильного тетраэдра одна грань серая. Тетраэдр серой гранью поставили на плоскость в треугольнике с надписью START. Затем тетраэдр начали перекатывать через рёбра по пути, указанному на рисунке. На какой из треугольников снова впервые после старта тетраэдр встанет серой гранью?
A) A Б) B В) C Г) D Д) E
25

Часть многочлена пятой степени на рисунке не видна из-за чернильного пятна. Известно, что многочлен имеет (с учётом кратности) пять целых корней. На какую наибольшую степень (x – 1) делится данный многочлен?
A) (x – 1)1
Б) (x – 1)2
В) (x – 1)3
Г) (x – 1)4
Д) (x – 1)5
26
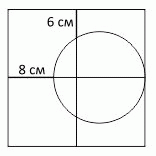
Квадрат на рисунке разбит на четыре меньших квадрата. Окружность касается правой стороны квадрата в её середине. Какую длину имеет сторона исходного квадрата? (Обратите внимание, что схема нарисована не в масштабе.)
A) 18 см Б) 20 см В) 24 см Г) 28 см Д) 30 см
27
Чему равен наибольший общий делитель всех чисел вида
n3 (n + 1)3 (n + 2)3 (n + 3)3 (n + 4)3
при всех натуральных n?
A) 29 33
Б) 23 33 53
В) 26 33 53
Г) 28 32 53
Д) 29 33 53
28
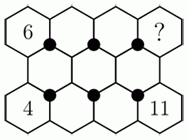
Числа от 1 до 11 нужно вписать в ячейки на рисунке так, чтобы суммы трёх чисел вокруг каждой из шести чёрных отмеченных точек были одинаковы. Три числа уже вписаны, как показано на рисунке. Какое число должно быть вписано в ячейку со знаком вопроса?
A) 1 Б) 3 В) 5 Г) 7 Д) 9
29
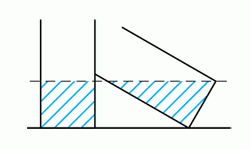
Два одинаковых цилиндрических резервуара для воды содержат одинаковое количество воды. Один цилиндр стоит вертикально, а другой прислонен к нему, и уровни воды в них одинаковые (см. рис.). Дно каждого из цилиндров представляет собой круг площадью 3π м2. Сколько воды находится в каждом из резервуаров?
A) 3√3π м3
Б) 6π м3
В) 9π м3
Г) 3/4 π м3
Д) недостаточно данных, чтобы определить однозначно
30
Произведение шести последовательных чисел равно 12-значному числу вида
abb cdd cdd abb,
где цифры a, b, c и d сами являются четырьмя последовательными числами в некотором порядке.
Каково значение цифры d?
A) 1 Б) 2 В) 3 Г) 4 Д) 5